Todo sobre el origami

origami

El origami (折り紙^?) es el arte de origen japonés consistente en el plegado de papel para obtener figuras de formas variadas. En español se denomina usualmente papiroflexia, aunque su nombre oriental (origami) también está muy extendido. Otra palabra para referirse a este arte es cocotología.En el origami no se utilizan tijeras ni pegamento o grapas, tan sólo el papel y las manos. Aún así, con sólo algunas hojas de papel pueden obtenerse distintos cuerpos geométricos (inclusopoliedros) y figuras parecidas a la realidad (animales, personas, flores, objetos, etc). Las distintas figuras obtenidas a partir de una hoja de papel pueden presentar diferentes áreas (según la porción de papel que queda debajo de otra) y varios volúmenes.

TIPOS DE ORIGAMI

Origami de acción

El origami no sólo representa figuras inmóviles, también existen objetos móviles donde las figuras pueden moverse de maneras ingeniosas. El origami de acción incluye modelos que vuelan, que requieren ser inflados para completarlos o que presionando o tirando de cierta región del modelo se consigue que la figura mueva un miembro, aletee, etc. Algunos sostienen que, en realidad, sólo este último es realmente “reconocido” como origami de acción. El origami de acción, habiendo aparecido primero con el pájaro aleteador japonés tradicional, es bastante común. Un ejemplo son los instrumentalistas de Robert Lang; cuando se hallan las cabezas de las figuras en sentido contrario a sus cuerpos, sus manos se moverán, asemejándose a la acción de tocar música.

Origami modular (Kusudama)

El origami modular consiste en poner una cantidad de piezas idénticas juntas para formar un modelo completo. Las piezas son normalmente simples pero el conjunto final puede ser complicado. Muchos de los modelos modulares de origami son bolas decorativas como el kusudama, sin embargo la técnica difiere en que el kusudama permite que las piezas sean puestas juntas usando hilo o pegamento.

La papiroflexia china incluye un estilo llamado "Origami 4D" donde una gran cantidad de piezas se juntan para hacer modelos elaborados. A veces se utilizan billetes para los módulos. Este estilo fue creado por algunos refugiados chinos mientras fueron detenidos en América y se conoce también como "Golden Venture" en honor al barco en el que viajaron.

El plegado en húmedo 

es una técnica de origami para producir modelos con curvas finas en vez de pliegues geométricos rectos y superficies planas. Consiste en humedecer el papel para que pueda ser moldeado fácilmente. El modelo final mantiene su forma cuando se seca. Puede ser utilizado por ejemplo para producir modelos de animales de apariencia muy natural.Pureland origami
Se trata de un estilo en el que solamente se puede hacer un pliegue a la vez y no se permiten pliegues más complejos como los invertidos. Todos los pliegues deben tener localizaciones directas. Fue desarrollado por John Smith en los años 70 para ayudar a plegadores novatos o a aquellos con habilidades motoras limitadas. A algunos diseñadores también les gusta el desafío de crear buenos modelos dentro de límites tan estrictos.

TECNICAS DE DISEÑO

Empaquetado de círculos

Todas las técnicas de diseño enfocan el diseño de la figura pensando en la figura desdoblada, una hoja cuadrada con todos los dobleces valles y montes en ella, lo que se denomina comocrease pattern o patrón de doblado (uno de ellos se puede ver en la figura de los teoremas y axiomas del origami)

Existen muchas técnicas de diseño, entre las cuales Robert Lang clasifica en:

División de puntos: Del inglés splitting points. Consiste en dividir una solapa en dos o más solapas dividiendo un punto. La desventaja es que las solapas finales son más cortas que la original. Es muy útil para crear dedos en patas o manos de seres vivos. ¹

Injerto: Del inglés grafting. Consiste en ampliar las características de una base añadiéndole otras. A partir de un cuadrado principal añadimos cuadrado más pequeños en las esquinas, como la figura resultante no es practica, se toma un cuadrado de papel que los contiene a todos. El cuadrado principal será una base principal, los demás serán bases secundarias. El resultado es una base final más compleja que añade características adicionales al diseño básico. Por lo general la técnica produce desperdicio de papel ^2 3 4

Injerto de patrones: Del inglés pattern Grafting. A un modelo básico se le añade un patrón regular, un dobles típico repetido muchas veces que da un efecto profesional. por ejemplo escamas en peces, dragones y caparazones en tortugas.

mosaico: Del inglés tiling. Consiste en observar la figura a diseñar y descomponerla en sus bloques más básicos (baldosas) compuestos generalmente por triangulos con dobleces internos. La punto de vista al abordar el problema de diseño es que la hoja de papel no es una sola unidad sino varias unidades flexibles, triángulos que pueden ser separados, rectángulos o ríos que pueden injertarse. Una forma de abordar el problema es imaginar la figura final con un diagrama de palos o segmentos. Despues dibujar en el cuadrado los círculos y los ríos (se denominan así porque parecen ríos de papel sin doblar, en medio de los círculos y semicírculos). Posteriormente estudiar el doblado de cada "baldoza" del mozaico para que calce con las otras y de origen a una secuencia de doblado exitosa.

Empaquetamiento de círculos: Del inglés Circle packing. Cuando se desea construir una nueva figura lo primero que se debe hacer es contar el número de solapas que tendrá , por ejemplo si se quisiera diseñar un perro este tiene una cabeza, una cola y cuatro patas, por lo tanto la figura debe tener 6 solapas. Cada solapa tiene un largo del radio de un círculo. En el inicio del diseño en el papel cuadrado se dibujan estos 6 círculos con la restricción de que sus centros siempre queden dentro del papel y que no se superponga un círculo con otro (ver figura). Después se conectan los centros de los círculos contiguos con un doblez. Posteriormente se añaden dobleces secundarios. Finalmente se encuentra una secuencia de doblado que origine el patrón de dobleces. Se consigue así una base para la figura quedando por añadir tan sólo los detalles.

Moléculas: Del inglés molecules. La moléculas son polígonos, triángulos, cuadrilateros, pentágonos los cuales si se juntan esta asegurado que la figura podrá doblarse y colapsarse dando origen a la figura final. Si se diseño por empaquetamiento de círculos entonces las moléculas son la solución para establecer un patrón de doblado de valles y montes.

Teoría del árbol: Del inglés tree theory. Se basa en enfocar el diseño dibujando la figura final como un árbol con ramas, en que cada rama es una solapa. Posteriormente esto dará origen a círculos y ríos en la hoja de papel.

Matemáticas en el origami

Teorema de Maekawas
Ya desde la misma invención del papel se estaba haciendo ciencia sin saberlo, por casualidad, pero la tecnología, buscaba por necesidad un producto flexible y duradero para escribir. Tratando de encontrar sus funcionalidades le inspiró al hombre este invento.
El origami también tiene una vertiente científica, dependiendo de las preferencias de cada plegador, o de su sistema de creación. Los pliegues no son más que operaciones de simetría, a veces bastante complejas, y pueden ser ideadas y estudiadas metodológicamente en términosgeométricos. El carácter matemático que pueda tener el plegado de papel no está reñido con el lado artístico, aunque tampoco tiene por qué coincidir. Por ejemplo del aspecto científico del origami, podemos mencionar a los aficionados que se dedican a demostrar teoremas geométricos utilizando sólo el papel y las hipótesis a punto de ser teoremas, incluso hay trabajos publicados sobre la resolución de ecuaciones de 3^er grado sólo doblando el papel. Como consecuencia lógica de este campo es la versatilidad que ha dado el origami a la enseñanza en las clases de matemáticas a nivel preuniversitario. Además, el origami ofrece un ingrediente especial, en tanto se incentive al practicante a crear sus propios modelos, se estará despertando y fomentando la curiosidad científica, ya que, como las matemáticas, el origami es infinito.
En los últimos 30 años se han realizado grandes avances en el plegado de figuras por la incorporación de artistas con conocimiento matemáticos, los cuales han creado teoremas y técnicas para diseñar de la forma más eficiente posible con respecto al uso del papel. Es sorprendente lo tardío de estos avances ya que muchos de los teoremas son problemas resueltos y conocidos en el campo de la geometría. Otros como el uso del lagrangeano para minimizar una función sujeta a restricciones es ampliamente sabido desde muchisimos años atrás, pero que no había sido utilizada para resolver diseños de figuras plegadas en papel. Inicialmente los artistas probaban a dar con la figura segun su experiencia, ocupando bases típicas sin recurrir a las matemáticas. Actualmente basta aplicar una metodología específica para llegar a nuevas formas. Esta metología se establece con ayuda de teoremas que resumen lo que es o no es posible llevar a cabo.
Se han realizado numerosos estudios matemáticos acerca del arte del plegado de papel papiroflexia u origami. Los aspectos que han despertado interés matemático incluyen la capacidad de aplastar sin dañar una determinada figura de papel (problema conocido como flat-foldability, o doblez plana), y el uso de dobleces de papel para resolver ecuaciones matemáticas.
Se ha demostrado que algunos problemas geométricos de construcción clásicos, como trisecar un ángulo cualquiera o duplicar el volumen de un cubo cualquiera, no se pueden resolver utilizando regla y compás, pero se pueden resolver bastante fácilmente con unos pliegues de papel. Se pueden realizar pliegues de papel para resolver ecuaciones de hasta cuarto grado y ecuaciones polinomiales – las cuales sólo contienen términos del tipo a_nxⁿ– (los aximomas de Huzita-Hatori son una importante contribución a este campo de estudio).
Como resultado del estudio del Origami a través de la aplicación de principios de geometría, métodos como el Teorema de Haga han permitido doblar precisamente el lado de un cuadrado en tres, cinco, siete y nueve partes. Otros teoremas y métodos han permitido derivar otras formas a partir de un cuadrado, tales como triángulos equiláteros, pentágonos, hexágonos, y rectángulos de características especiales tales como el rectángulo dorado o el rectángulo de plata.
El problema del origami rígido, que trata los pliegues como líneas que unen dos superficies planas rígidas tales como pletinas, tiene gran importancia práctica. Por ejemplo, el pliegue de mapa de Miura es un pliegue rígido que se ha utilizado para desplegar grandes paneles solares de satélites espaciales.
La obtención de un modelo plano a partir de un patrón arrugado es un proceso que Marshall Bern y Barry Hayes han demostrado que es NP-completo. [1] Se discuten referencias adicionales y resultados técnicos en la Parte II de Geometric Folding Algorithms. ⁵La función de pérdida de doblar un papel en dos en una única dirección se ha determinado como 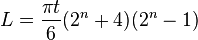, dondeL es la longitud mínima del papel (u otro material), t es el grosor del material, y n es el número de pliegues posibles. Esta función fue publicada por Britney Gallivan en 2001 (por entonces todavía estudiante de secundaria, que logró doblar una hoja de papel por la mitad 12 veces. Hasta entonces se había creído popularmente que el papel de cualquier tamaño no podía doblarse más de 8 veces.
Algunos de los teoremas son:

1. Teorema de Maekawas: señala que la diferencia entre montes y valles debe ser siempre 2.

1. Teorema de Kawasaki: Todos los vertices interiores suman 180

1. Axioma 1: Dados dos puntos P y Q se puede realizar el pliegue que los une. Un único pliegue pasa por 2 puntos P y Q específicos

1. Axioma 2: Dados dos puntos P y Q se puede realizar el pliegue que sitúa a P sobre Q. En otras palabras un único pliegue lleva a un punto P sobre un punto Q.

1. Axioma 3: Dado un punto P y una recta r se puede realizar el pliegue perpendicular a r que pasa por P

1. Axioma 4: Dadas dos rectas r y s se puede realizar un pliegue que situe a r sobre s.

1. Axioma 5: Dados dos puntos P y Q y una recta r podemos realizar un pliegue que situe a P sobre r y pase por Q.

1. Axioma 6: Dados dos puntos P y Q y dos rectas r y s se puede realizar un pliegue que sit´ue a P sobre r y a Q sobre s.

También existen axiomas relacionados con la gemetría del origami definidos por Humiaki Huzita, basados en 6 pliegues básicos que permiten analizar la geometría de cualquier origami:
El origami además de crear sus propias reglas relacionadas a la geometría Euclideana, también brinda a la educación una herramienta importante para mejorar las capacidades de concentración, memoria, análisis y desarrollo de conceptos geométricos por medio de la activación del pensamiento lógico-espacial y el desarrollo de las destrezas psicomotrices.

EN EL SIGUIENTE VIDEO MUESTRO

 COMO ASER UNA FIGURA DE PAEL EN 

ORIGAMI.